SOFAStack(Scalable Open Financial Architecture Stack) 是蚂蚁金服自主研发的金融级云原生架构,包含了构建金融级云原生架构所需的各个组件,是在金融场景里锤炼出来的最佳实践。

SOFAJRaft 是一个基于 Raft 一致性算法的生产级高性能 Java 实现,支持 MULTI-RAFT-GROUP,适用于高负载低延迟的场景。
本文作者胡宗棠,SOFAJRaft Committer,来自中国移动。本文主要介绍 SOFAJRaft 在 Leader 选举过程中的重要优化方案—一种半确定性的优先级选举机制,将会先简单地介绍下原 Raft 算法中随机超时选举机制的大致内容,如果读者对这块内容理解得不够深入,建议可以先阅读下《SOFAJRaft 选举机制剖析 | SOFAJRaft 实现原理》。阅读完这篇文章后,再来看本篇的内容会对半确定性的优先级选举机制有更为深刻的理解。
SOFAJRaft:https://github.com/sofastack/sofa-jraft
一、Raft 算法中选举机制的概念与特点
Raft 算法是一种“共识性”算法,这里所谓的“共识性”主要体现在让多个参与者针对某一件事达成完全一致:一件事一个结论,同时对已达成一致的结论,是不可推翻的。基于这个根本特征,就决定了 Raft 算法具有以下几个主要特点:
- Strong leader:Raft 集群中最多只能有一个 Leader,日志只能从 Leader 复制到 Follower 上;
- Leader election:Raft 算法采用随机超时时间触发选举来避免选票被瓜分的情况,保证选举的顺利完成。这是主要为了保证在任何的时间段内,Raft 集群最多只能存在一个 Leader 角色的节点;
- Membership changes:通过两阶段的方式应对集群内成员的加入或者退出情况,在此期间并不影响集群对外的服务;
在 Raft 算法中,选举是很重要的一部分。所谓选举就是在由多个节点组成的一个 Raft 集群中选出一个 Leader 节点,由他来对外提供写服务 (以及默认情况下的读服务)。
这里先介绍一个任期的概念—Term, 其用来将一个连续的时间轴在逻辑上切割成一个个区间,它的含义类似于“美国第 26 届总统”这个表述中的“26”。同时,该 Term ID 的值是按照时间轴单调递增的,它构成了 Raft Leader 选举的必要属性。
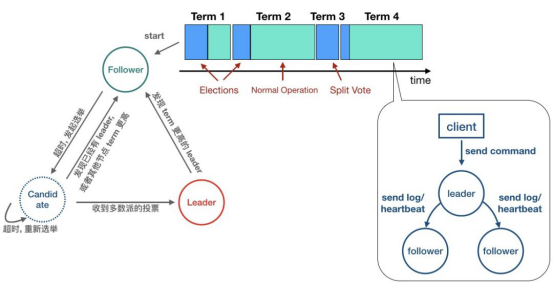
每一个 Term 期间集群要做的第一件事情就是选举 Leader。起初所有的 Server 都是 Follower 角色,如果 Follower 经过一段时间( election timeout )的等待却依然没有收到其他 Server 发来的消息时,Follower 就可以认为集群中没有可用的 Leader,遂开始准备发起选举。为了让 Raft 集群中的所有节点尽可能的客观公平公正,采用了随机超时时间触发选举,来避免若干个节点在同一时刻尝试选举而导致选票被瓜分的情况,保证选举的顺利完成。SOFAJRaft 的做法是,在 Node 触发选举的定时任务— electionTimer 中的设置每次定时执行的时间点:时间区间 [electionTimeoutMs,electionTimeoutMs + maxElectionDelayMs) 中的任何时间点。
在发起选举的时候 Server 会从 Follower 角色转变成 Candidate,然后开始尝试竞选 Term + 1 届的 Leader,此时他会向其他的 Server 发送投票请求,当收到集群内多数机器同意其当选的应答之后,Candidate 成功当选 Leader。但是如下两种情况会让 Candidate 退回 (step down) 到 Follower,放弃竞选本届 Leader:
- 如果在 Candidate 等待 Servers 的投票结果期间收到了其他拥有更高 Term 的 Server 发来的投票请求;
- 如果在 Candidate 等待 Servers 的投票结果期间收到了其他拥有更高 Term 的 Server 发来的心跳;
同时,当一个 Leader 发现有 Term 更高的 Leader 时也会退回到 Follower 状态。当选举 Leader 选举成功后,整个 Raft 集群就可以正常地向外提供读写服务了,如上图所示,集群由一个 Leader 和两个 Follower 组成,Leader 负责处理 Client 发起的读写请求,同时还要跟 Follower 保持心跳和将日志 Log 复制给 Follower。
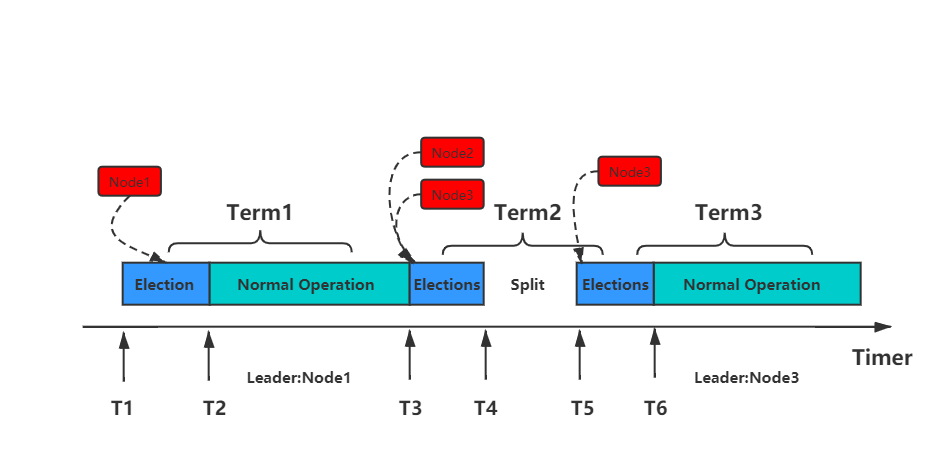
但 Raft 算法的“随机超时时间选举机制”存在如下问题和限制:
- 下一个任期 Term,Raft 集群中谁会成为 Leader 角色是不确定的,集群中的其他节点成为 Leader 角色的随机性较强,无法预估。试想这样的一个场景:假设部署 Raft 集群的服务器采用不同性能规格,业务用户总是期望 Leader 角色节点总是在性能最强的服务器上,这样能够为客户端提供较好的读写能力,而上面这种“随机超时时间选举机制”将不能满足需求;
- 如上图所示,由于会存在选票被瓜分的场景,集群中的各个 Candidate 角色节点将在下一个周期内重新发起选举。而在这个极短的时间内,由于集群中不存在 Leader 角色所以是无法正常向客户端提供读写能力,因此业务用户需要通过其他方式来避免短时间的不可用造成的影响;
二、SOFAJRaft 基于优先级的半确定性选举机制
2.1 SOFAJRaft 基于优先级选举机制的原理
为了解决原本 Raft 算法“随机超时时间选举机制”带来的问题,增加选举的确定性,作者贡献了一种“基于优先级的半确定性选举机制”。主要的算法思想是:通过配置参数的方式预先定义 Raft 集群中各个节点的 priority 选举优先级的值,每个 Raft 节点进程在启动运行后是能够知道集群中所有节点的 priority 的值(包括它自身的、本地会维护 priority 变量)。
对每个 Raft 节点的配置如下(下面以其中一个节点的配置举例),其中 PeerId 的字符串值的具体形式为:{ip}:{port}:{index}:{priority};
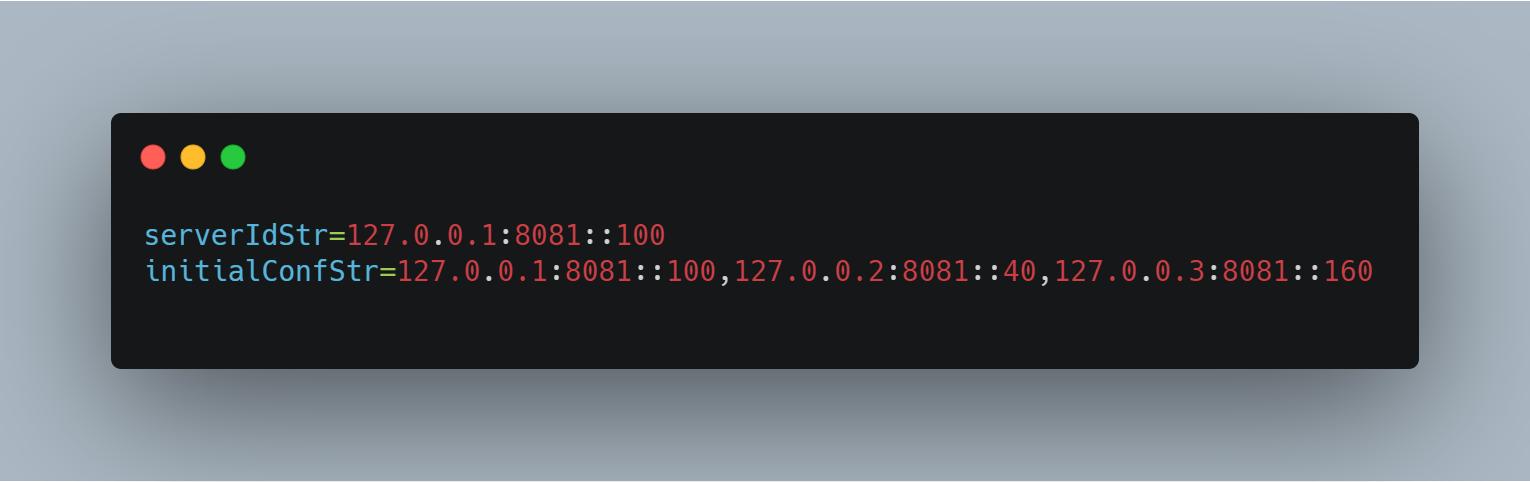
在 Raft 节点进程初始化阶段,通过对所有节点 priority 值求最大值来设置至节点自身维护的 targetPriority 本地全局变量里。在上面这个例子中,节点的 targetPriority 本地全局变量值就被设置为 160,而自身的 priority 值为 100。
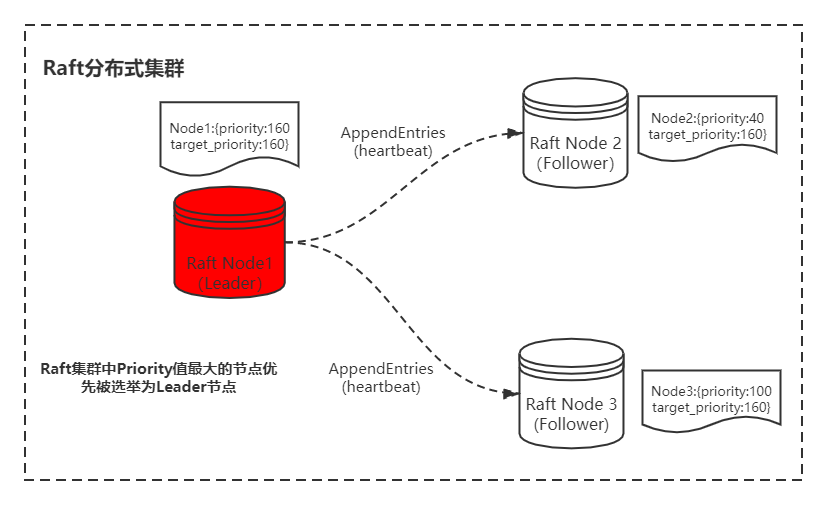
在每个 Raft 节点通过随机超时机制触发 PreVote 预选举阶段之前,会通过先比较自身的 priority 值和 targetPriority 值来决定是否参加本轮的 Leader 选举投票。所以,一组 Raft 节点组成的集群在刚启动运行的阶段,priority 值最大的节点(上面例子中 160 的那个节点)必然会优先被选择成为这个集群中 Leader 角色的节点向外提供读和写的服务。
2.2 SOFAJRaft 优先级选举在故障情况下的重选举机制
在大部分正常的业务场景中,Raft 集群中的 Leader 角色节点是可以通过上面 2.1 节中介绍的方法来预先确定的。但在实际的生产环境中,一切未知情况都有可能发生,如果 Raft 集群中的 Leader 节点发生故障宕机,那么基于上述内容的优先选举是否就会出现问题了?
可以想到,priority 值最大的节点宕机后,如果其他各个节点维护的本地全局变量 targetPriority 值如果不发生改变,因为节点自身的 priority 值是小于前者的,那其他 Raft 节点不就永远都无法来参与竞选 Leader 角色,没有 Leader 节点整个 Raft 集群也就无法向外提供读写服务了,这将是设计中的重大缺陷问题!!!
为了解决上述 Raft 集群在发生故障转移时,其他节点无法参与竞选新 Leader 角色的问题。作者在设计时,引入了 “decayTargetPriority()” 目标优先级衰减降级函数,如果在上一轮由随机超时时间触发的选举周期内没有投票选出 Leader 角色,那么 Raft 集群中其他各个节点会对本地全局变量 targetPriority 的值按照每次减少 20% 进行衰减,直至衰减值优先级的最小值“1”。目标优先级衰减降级函数的源码如下:
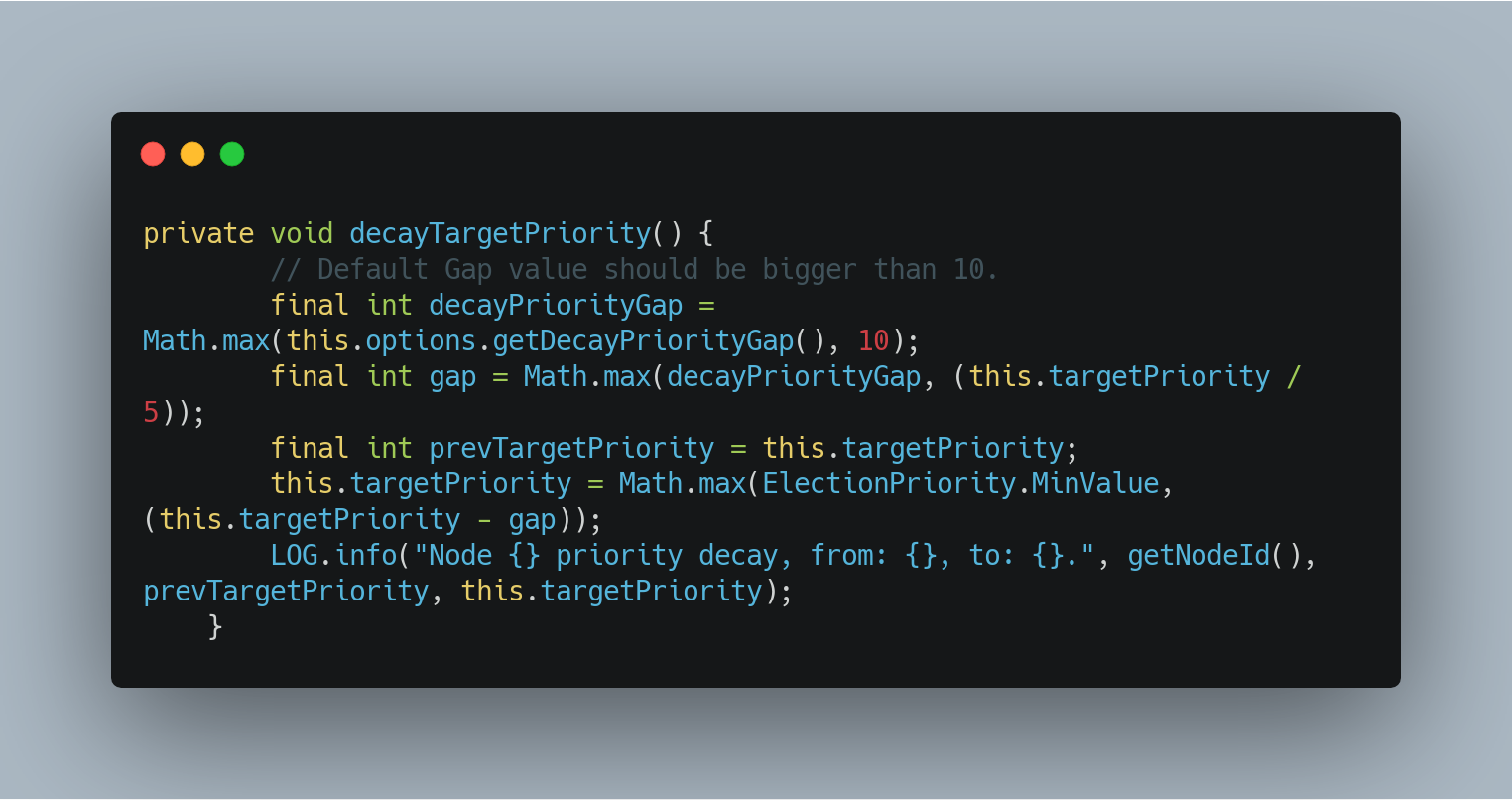
当其他节点在对自身维护的本地全局变量 targetPriority 进行衰减后,如果节点自身的 priority 值大于等于 targetPriority 值,则该节点能够参与到由随机超时时间触发的下一轮 Leader 选举流程中。在一般的情况下,次优先级值的节点能够抢占到下一轮 Leader 选举的机会。
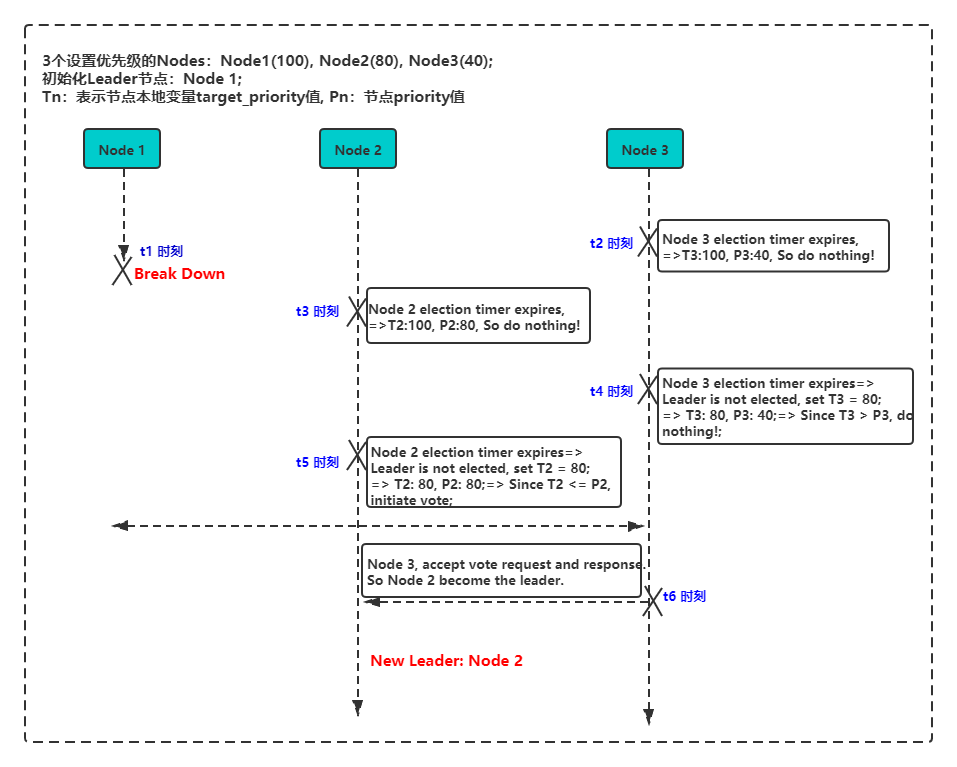
如上面时序图所示,当 Raft 集群出现 Leader 角色的 Node1 节点宕机异常情况时,由于 Node2 和 Node3 无法与之同步心跳信息,这两个节点会通过随机超时时间触发新 Leader 的选举流程。
在假设在 t2(>t1)时刻,Node3 抢先触发了 Leader 选举流程,因为其自身的 priority 值(40)小于本地全局 targetPriority 变量值(100),所以无法发起向 Raft 集群中其他存活的节点发起 PreVote 预投票请求。
同理,在 t3(>t2)时刻,Node2 也同 Node3 一样无法发起 PreVote 预投票请求。但当到了 t4(>t3)时刻,由于在上一个选举周期内 Raft 集群中没有产生 Leader 角色节点,所以会将其本地全局变量 targetPriority 值进行 20% 的衰减(如上图中“set T3 = 80”),经过衰减后由于 Node3 的 priority 值仍然是小于衰减后的 targetPriority 变量值(80),所以还是无法发起投票请求。
同理,在 t5(>t4)时刻,Node2 在经过衰减后其 targetPriority 值(80)等于自身的 priority 值(80),因而可以向 Raft 集群中其他节点发起 PreVote 预投票请求,得到 Node3 的响应后,Raft 集群就产生了新的 Leader 角色节点 — Node2。
由于 Node 触发选举的定时任务 — electionTimer,每次随机超时触发的执行时间点不确定,在如上图所示的实际应用场景中,Node2 或 Node3 都有可能会抢先执行目标优先级衰减降级的流程,所以如果 Node2 和 Node3 自身的 priority 值设置的比较接近,比如 Node3 和 Node2 的 priority 值分别设置为 50 和 40,那么在某一些时刻,优先级小的 Node2 也有可能会成为 Raft 集群中的 Leader。因此,在实际的生产环境使用中,建议将 Raft 集群中各个节点的优先级定义成区分度较高的数值。
三、SOFAJRaft 优先级选举机制的实践示例
在 SOFAJRaft 的 GitHub上有比较详细的 example 示例,链接: https://github.com/sofastack/sofa-jraft/tree/master/jraft-example/src/main/java/com/alipay/sofa/jraft/example/priorityelection
其中的启动代码如下:
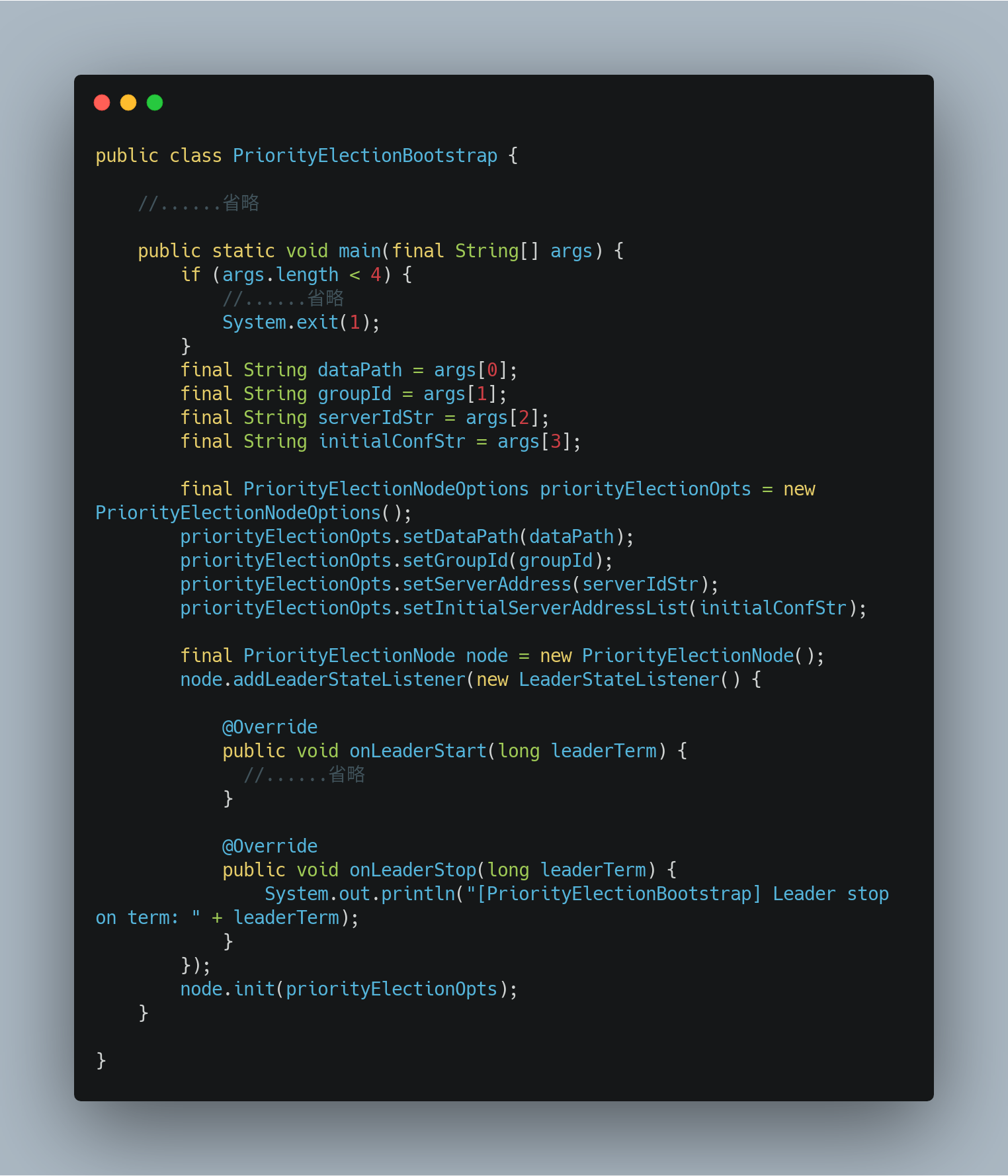
感兴趣的用户可以在本地编辑环境,比如 Idea 或者 Eclipse 的运行命令行中将上面的 demo 程序中所需要的参数设置完,即可体验优先级选举的实际效,其中与优先级选举相关的配置参数在 NodeOptions 类中。
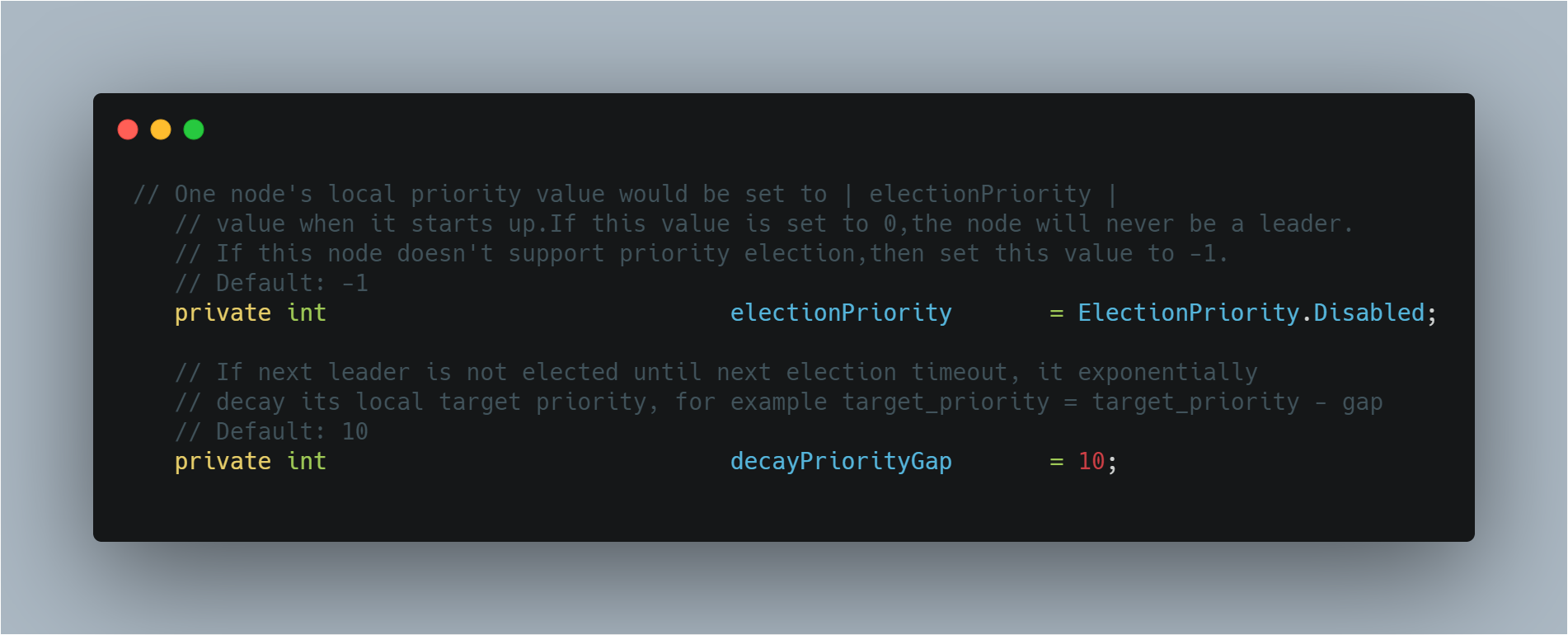
如上图所示,其中:
- electionPriority:Node 节点本身的 priority 值。如果设置为 0,则表示该节点不参与 Raft 集群 Leader 角色的选举流程,它永远不会成为 Leader 角色;如果设置为 -1,则表示该节点不支持优先级选举功能,它还是执行原本 Raft 随机超时时间选举流程;
- decayPriorityGap:优先级衰减的间隔值,如果用户认为 Node 节点本身的 priority 值衰减过慢,可以适当地增加该配置参数,这样可以使得 priority 值较小的节点不需要花费太多时间即可完成衰减;
四、 SOFAJRaft 优先级选举机制的源码解析
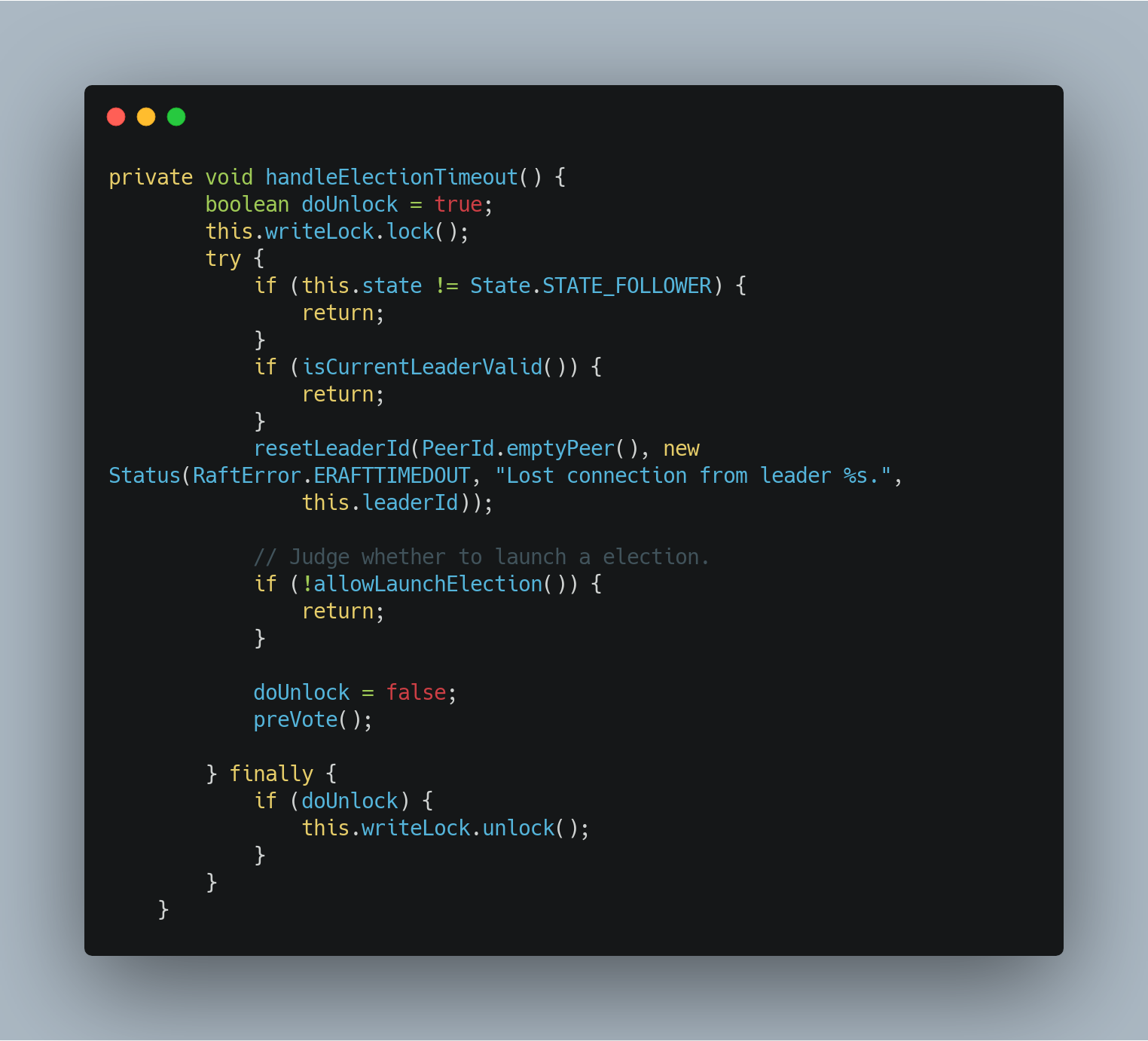
如上图所示,在 SOFAJRaft 随机超时时间触发的定时任务— JRaft-ElectionTimer-X,所执行的 handleElectionTimeout() 方法中,在 preVote 预投票前通过对当前 Node 的优先级变量 priority 值与本地全局变量 targetPriority 值进行判断和比较,来决定当前 Node 节点是否参与 Raft 集群本轮 Leader 角色的选举流程。
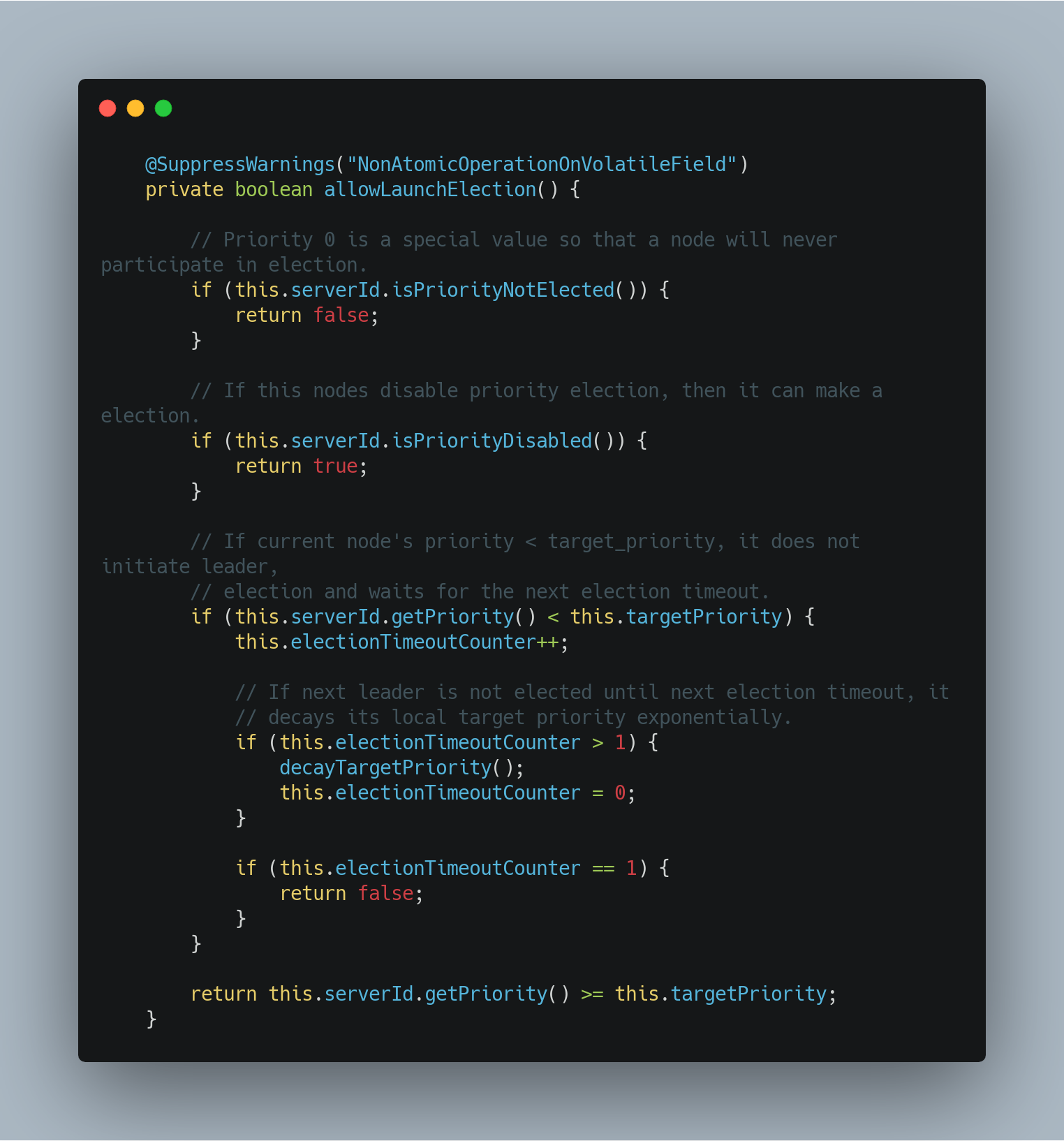
allowLaunchElection() 方法中定义了当前 Node 节点判断 priority 值与本地全局变量 targetPriority 值的逻辑。同时,如果在上一轮选举周期内没有选举出 Leader 角色的节点,那么执行目标优先级衰减降级方法,并设置相关的变量值。
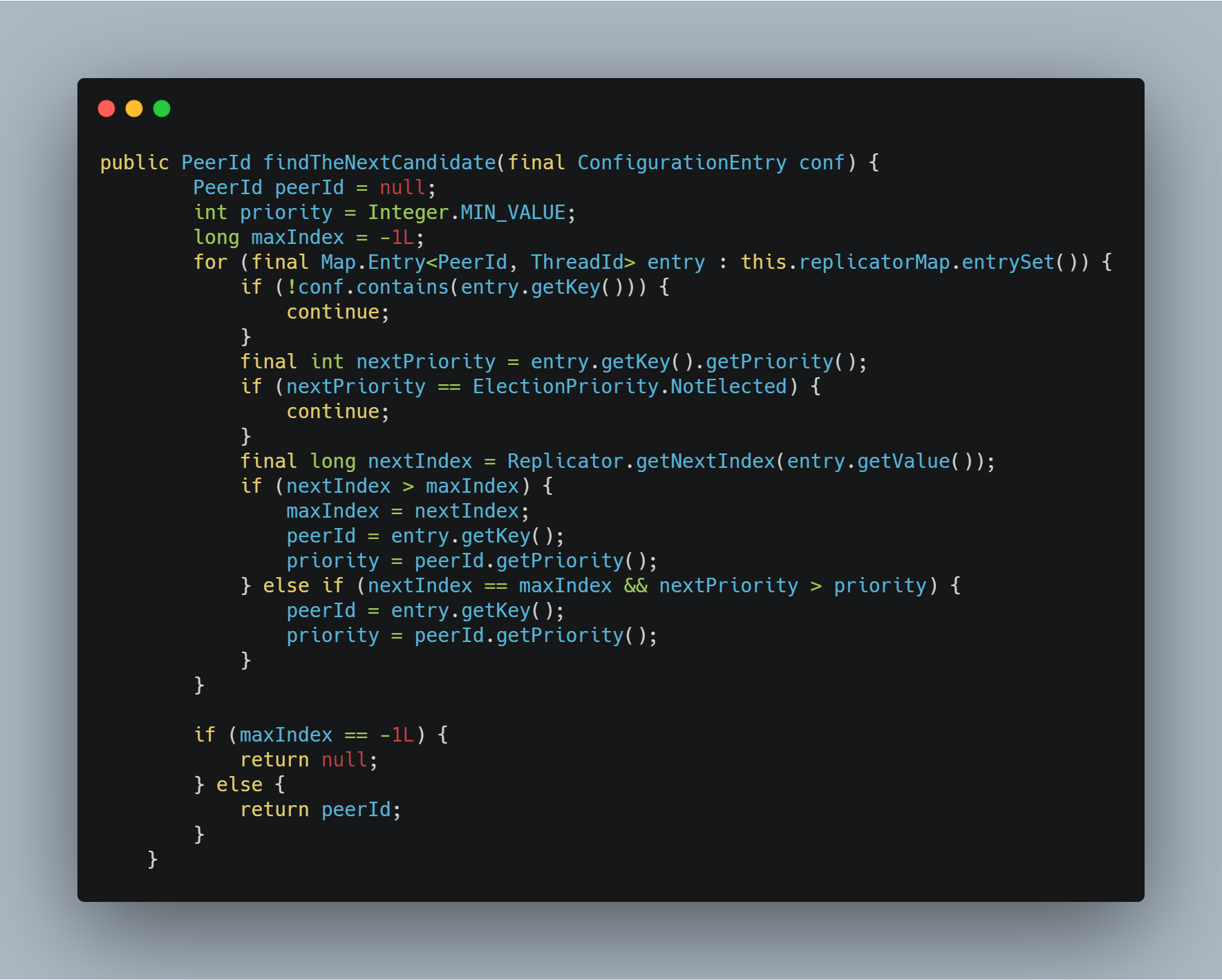
另外,还有一个问题需要注意,在 NodeImpl 中的 stepDown() 方法会调用stopAllAndFindTheNextCandidate() 方法去暂停所有日志复制的 Replicator 线程,同时找到下一个具有最完备日志的节点作为最后可能接任下一任 Leader 角色的 Candicate 候选人。所以引入优先级选举的概念后,除了需要比较日志的 log_index 值大小以外,如果两个节点的 log_index 值是相等的,那么还需要再判断 priority 值。具体的代码如下所示:
五、SOFAJRaft 优先级选举机制的 Jepsen 测试
Jepsen 能在特定故障下验证系统是否满足一致性,一方面它提供了故障注入的手段,能模拟各种各样的故障,比如网络分区,进程崩溃、CPU 超载等。另一方面,它提供了各种校验模型,比如 Set、Lock、Queue 等来检测各种分布式系统在故障下是否仍然满足所预期的一致性。所以,通过 Jepsen 测试,能发现分布式系统在极端故障下的隐藏错误,从而提高分布式系统的容错能力。
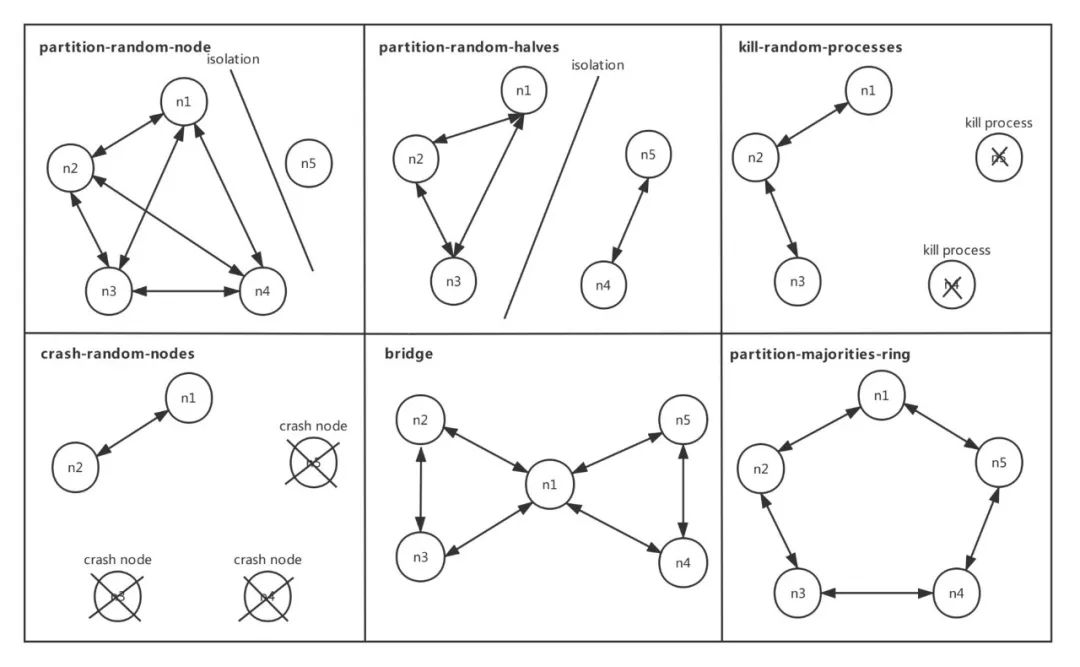
对于分布式系统而言,一般会使用如下几种类型的故障进行注入:
(1)partition-random-node 和 partition-random-halves 故障是模拟常见的对称网络分区; (2)kill-random-processes 和 crash-random-nodes 故障是模拟进程崩溃,节点崩溃的情况; (3)hammer-time 故障是模拟一些慢节点的情况,比如发生 Full GC、OOM 等; (4)bridge 和 partition-majorities-ring 模拟比较极端的非对称网络分区;
为验证 SOFAJRaft 优先级选举机制的可靠性,我们选择对上面(1)、(2)、(4)种类型的故障进行注入测试。以图表的形式可以更好分析 SOFAJRaft 集群在测试过程中的表现情况。下图展示的是,在模拟注入对称网络分区故障情况下,客户端对 SOFAJRaft 集群每一次操作的时延如下图所示:
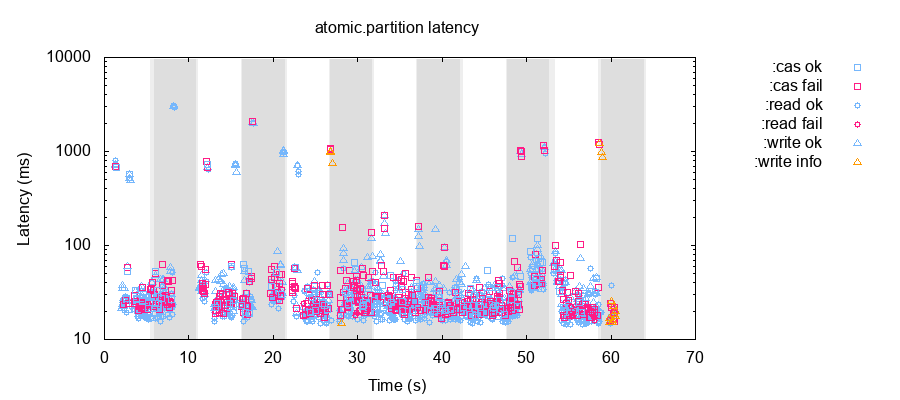
其中蓝色框表示数据添加成功,红色框表示数据添加失败,黄色框表示不确定是否数据添加成功,灰色部分表示故障注入的时间段。可以看出一些故障注入时间段造成了集群短暂的不可用,一些故障时间段则没有,这是合理的。由于是随机网络分区,所以只有当前 Leader 角色节点 被隔离到少数节点区域才会造成集群重新选举,但即使造成集群重新选举,在较短时间内, SOFAJRaft 集群也会恢复可用性。此外,可以看到由于 SOFAJRaft 对对称网络分区有较好的容错设计,每次故障恢复后,集群不会发生重新选举。
下图展示了 SOFAJRaft 在测试过程中时延百分位点图。
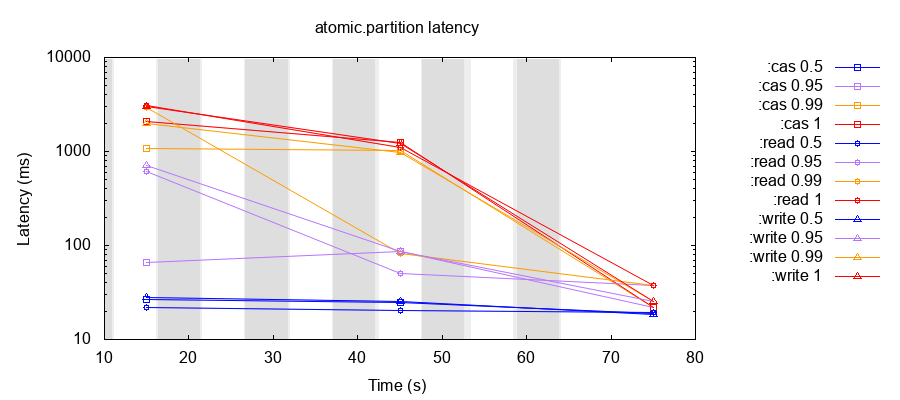
可以看到除了在一些故障引入后造成集群重新选举的时间段,时延升高,在其他的时间段, SOFAJRaft 集群表现稳定。 SOFAJRaft 在随机对称网络分区故障注入下,表现稳定,符合预期。除了随机对称网络分区, SOFAJRaft 在其他几种故障注入下也均通过了 Set 测试的一致性验证,证明了 SOFAJRaft 对网络分区,进程、节点崩溃等故障的容错能力和良好的可靠性。
六、总结
本文从原来 Raft 算法中随机超时选举机制带来的不确定性问题出发,围绕优先级选举机制的概念、特点和原理,并结合作者提出的 SOFAJRaft 优先级选举机制的设计和实现细节,详细阐述了其基本流程和半确定性,介绍了 SOFAJRaft 优先级选举的实践应用,并剖析了源码中的实现细节。
之前 SOFA 团队与社区同学共建完结了 《剖析 | SOFAJRaft 实现原理》系列,对 SOFAJRaft 的相关实现原理进行源码解析。现在开启《SOFAJRaft 特性解析》系列,本文为该系列的第一篇,后续也会持续展开对于 SOFAJRaft 特性的文章分享,也欢迎更多感兴趣的技术同学加入~
SOFAJRaft:https://github.com/sofastack/sofa-jraft
《剖析 | SOFAJRaft 实现原理》系列
- SOFAJRaft Snapshot 原理剖析 | SOFAJRaft 实现原理
- SOFAJRaft-RheaKV 分布式锁实现剖析 | SOFAJRaft 实现原理
- SOFAJRaft 日志复制 - pipeline 实现剖析 | SOFAJRaft 实现原理
- SOFAJRaft-RheaKV MULTI-RAFT-GROUP 实现分析 | SOFAJRaft 实现原理
- SOFAJRaft 选举机制剖析 | SOFAJRaft 实现原理
- SOFAJRaft 线性一致读实现剖析 | SOFAJRaft 实现原理
- SOFAJRaft 实现原理 - SOFAJRaft-RheaKV 是如何使用 Raft 的
- SOFAJRaft 实现原理 - 生产级 Raft 算法库存储模块剖析原理